Lesson 1: Understanding AMM Fundamentals
🎧 Lesson Podcast
🎬 Video Overview
Lesson 1: Understanding AMM Fundamentals
🎯 Core Concept: What is an Automated Market Maker?
An Automated Market Maker (AMM) is a decentralized exchange protocol that uses mathematical formulas instead of order books to determine prices and execute trades. Think of it as a robot market maker that's always ready to trade, 24/7, without needing human market makers or centralized exchanges.
Why AMMs Matter
Before AMMs, if you wanted to trade cryptocurrencies, you needed:
A centralized exchange (like Coinbase or Binance)
Market makers providing buy/sell orders
Trust in the exchange to hold your funds
AMMs changed everything by:
Eliminating intermediaries: No centralized exchange needed
Democratizing market making: Anyone can provide liquidity
Enabling permissionless trading: Trade any token pair, anytime
Creating composability: AMMs work with other DeFi protocols
📚 The Evolution: From Order Books to AMMs
Traditional Order Book Model
In traditional exchanges, prices are determined by matching buy and sell orders:
The "spread" ($2,010 - $2,000 = $10) is the profit margin for market makers. This model requires:
Active market makers providing constant quotes
Sufficient order depth for large trades
Centralized infrastructure
The AMM Revolution
AMMs replace order books with liquidity pools - smart contracts that hold reserves of two tokens. Prices are determined mathematically based on the ratio of tokens in the pool.
Key Innovation: Instead of waiting for someone to match your order, you trade directly against the pool's reserves.
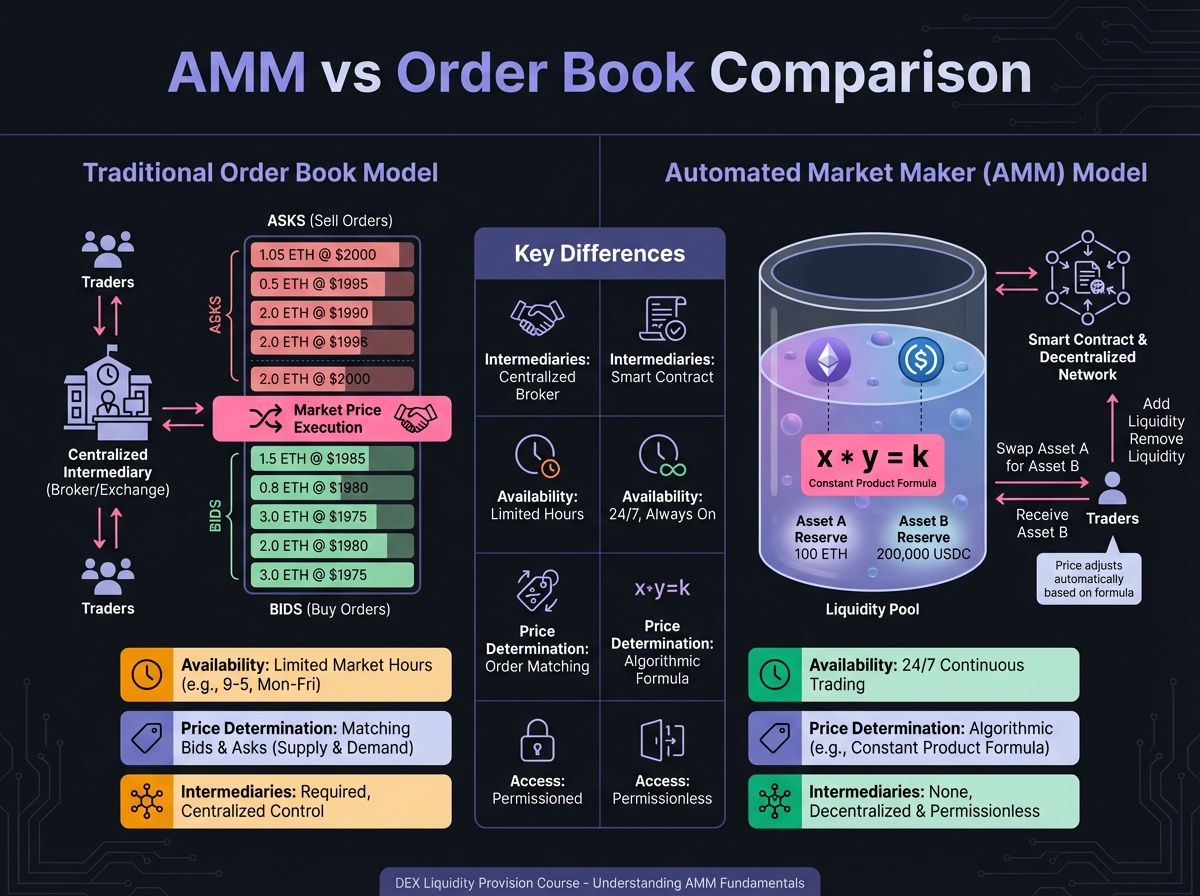
🔢 The Constant Product Formula: x · y = k
The foundation of most AMMs is the constant product formula, first popularized by Uniswap V2:
x⋅y=k
Where:
x = Reserve of token X (e.g., ETH)
y = Reserve of token Y (e.g., USDC)
k = Constant (must remain the same after every trade)
How It Works: A Simple Example
Imagine a pool with:
10 ETH (x = 10)
20,000 USDC (y = 20,000)
k = 10 × 20,000 = 200,000
Current Price: 20,000 USDC ÷ 10 ETH = 2,000 USDC per ETH
Scenario: Alice wants to buy 1 ETH
Alice deposits USDC into the pool
The pool calculates: To maintain k = 200,000, if x becomes 9 ETH, then y must become:
y = 200,000 ÷ 9 = 22,222 USDC
Alice must deposit: 22,222 - 20,000 = 2,222 USDC
New Price: 22,222 USDC ÷ 9 ETH = 2,469 USDC per ETH
Key Insight: The price moved up because Alice bought ETH, reducing the ETH supply in the pool. This is called "price impact" - larger trades move prices more.
Why "Constant Product"?
The formula ensures:
Liquidity always exists: As long as k > 0, you can always trade
Price discovery: Prices adjust automatically based on supply and demand
No slippage protection needed: The math handles it (though large trades still have impact)
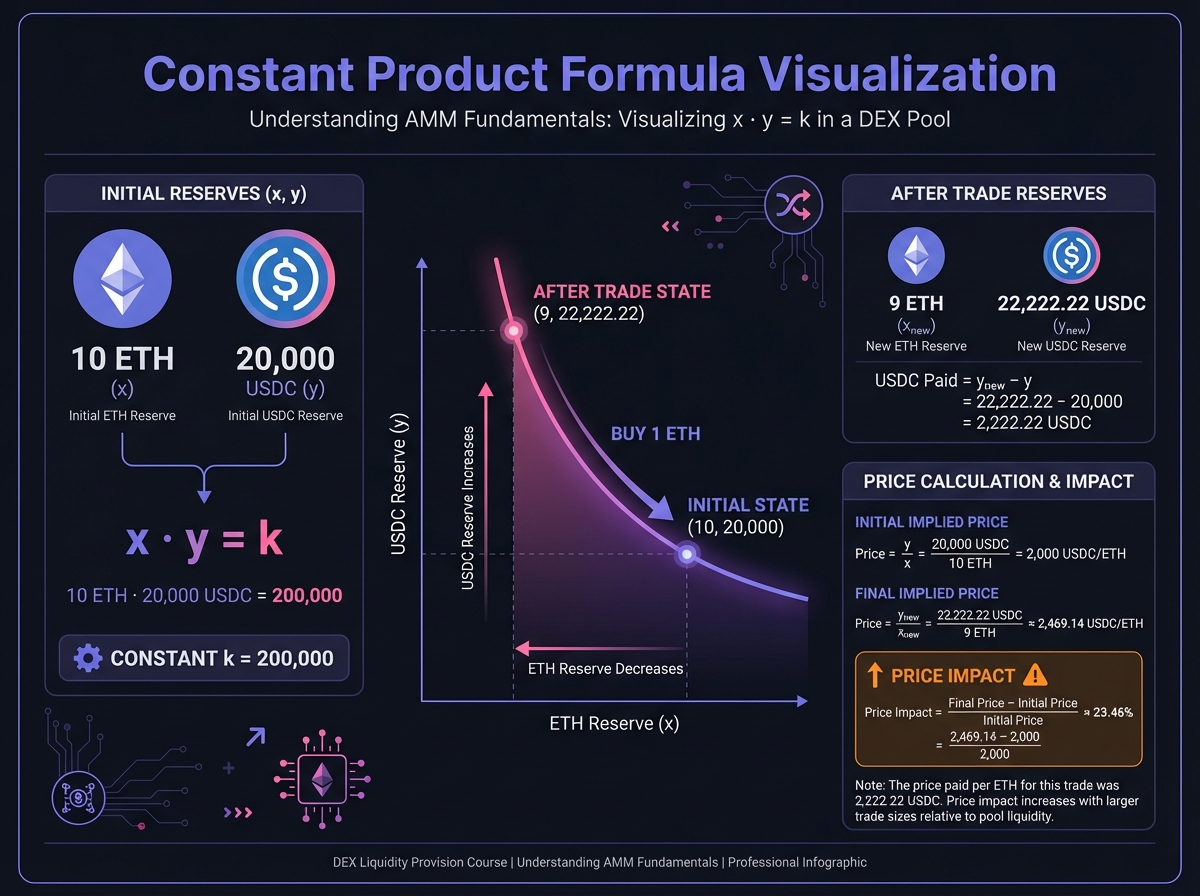
🏊 Understanding Liquidity Pools
A liquidity pool is a smart contract that holds two tokens in reserve. When you provide liquidity, you're depositing both tokens in equal value.
Pool Components
Token Pair: Two tokens (e.g., ETH/USDC, DAI/USDT)
Reserves: Current amounts of each token
Liquidity Providers (LPs): People who deposit tokens
Trading Fees: Usually 0.3% (0.05% for stablecoins) paid to LPs
LP Tokens: Receipt tokens representing your share of the pool
The Liquidity Provider's Role
When you provide liquidity:
You deposit equal values of both tokens
You receive LP tokens representing your share
You earn fees from all trades in the pool
You can withdraw your share anytime (plus fees earned)
Example:
Pool has 100 ETH and 200,000 USDC (total value: $400,000)
You deposit 1 ETH and 2,000 USDC (total value: $4,000)
You own 1% of the pool
You receive LP tokens representing 1% ownership
You earn 1% of all trading fees
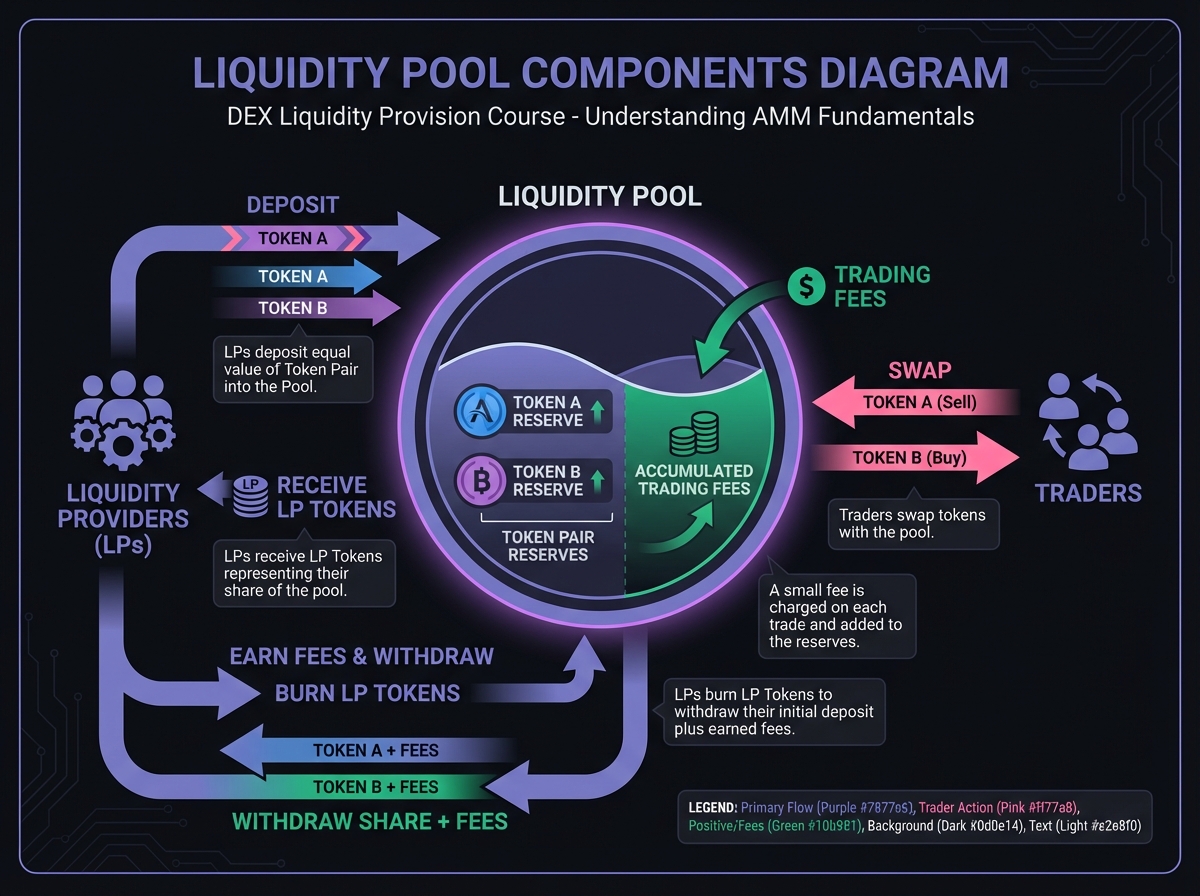
💰 How Fees Work
Every trade pays a fee (typically 0.3% for volatile pairs, 0.05% for stablecoins). This fee is:
Added to the pool: Increasing the value of LP tokens
Distributed proportionally: Based on your share of the pool
Auto-compounded: In V2, fees stay in the pool (in V3, they accumulate separately)
Fee Calculation Example:
Pool processes $1,000,000 in daily volume
Fee rate: 0.3%
Daily fees: $1,000,000 × 0.003 = $3,000
If you own 1% of the pool: $3,000 × 0.01 = $30/day
Annualized: $30/day × 365 = $10,950/year
On $4,000 investment = 273% APY (before considering impermanent loss!)
⚠️ Warning: High APY numbers are misleading. They don't account for impermanent loss, which we'll cover in Lesson 3.
🔄 The Trading Mechanism
Step-by-Step Trade Execution
Trader initiates swap: "I want to buy 1 ETH with USDC"
Smart contract calculates: Based on x · y = k formula
Price impact determined: Larger trades = more price movement
Tokens swapped: ETH removed, USDC added (or vice versa)
Fee collected: 0.3% added to pool reserves
New price set: Automatically by the new ratio
Price Impact and Slippage
Price Impact: How much the price moves due to your trade
Small trade (0.1% of pool): Minimal impact
Large trade (10% of pool): Significant impact
Slippage: The difference between expected and actual price
You expect: 1 ETH = 2,000 USDC
You get: 1 ETH = 2,050 USDC (after fees and impact)
Slippage: 2.5%
Protection: Most interfaces let you set maximum slippage tolerance (e.g., 1%). If slippage exceeds this, the trade fails.
🎓 Beginner's Corner: Common Questions
Q: Do I need to be a market maker to provide liquidity? A: No! AMMs make you a passive market maker. Just deposit tokens and earn fees.
Q: What if the pool runs out of tokens? A: The math ensures this never happens. As one token gets scarce, its price increases, making it expensive to buy more.
Q: Can I lose money providing liquidity? A: Yes. You can lose money through:
Impermanent loss (covered in Lesson 3)
Smart contract bugs
Token depegging (for stablecoin pairs)
Low trading volume (fewer fees)
Q: Which tokens should I pair? A: Start with:
Stablecoin pairs (USDC/USDT) - lowest risk
Correlated pairs (ETH/BTC) - moderate risk
Avoid volatile pairs initially - highest risk
🔬 Advanced Deep-Dive: The Mathematics Behind AMMs
Deriving the Constant Product Formula
The constant product formula ensures that the product of reserves remains constant:
x0⋅y0=x1⋅y1=k
Where subscripts 0 and 1 represent before and after a trade.
Price Calculation
The price of token X in terms of token Y is:
P=xy
This price changes with every trade, creating a continuous price curve.
Liquidity Depth
The "depth" of a pool determines how much you can trade before significant price impact. Depth is measured by:
D=x⋅y=k
Larger k = deeper pool = less price impact per trade.
Fee Integration
With fees, the formula becomes:
(x+Δx⋅(1−ϕ))⋅(y+Δy)=k
Where φ (phi) is the fee rate (e.g., 0.003 for 0.3%).
The fee is taken from the input token, so if you're buying ETH with USDC, the fee is deducted from your USDC before the swap calculation.
Capital Efficiency Problem
The fundamental issue with constant product AMMs is capital inefficiency:
For a stablecoin pair trading at $1.00, liquidity is spread from $0.01 to $100.00
99.9% of capital sits idle, earning no fees
Only a tiny fraction near the current price is active
This problem led to Uniswap V3's concentrated liquidity (covered in Lesson 5).
Interactive Slippage Impact Calculator
Use this interactive tool to calculate slippage impact for different trade sizes and understand how AMM mechanics affect prices:
Launch Slippage Impact Calculator →
📊 Real-World Example: Uniswap V2 ETH/USDC Pool
Let's examine a real pool to understand the mechanics:
Pool Stats (hypothetical):
Total Liquidity: 10,000 ETH + 20,000,000 USDC
Pool Value: $40,000,000
Daily Volume: $5,000,000
Fee Rate: 0.3%
Your Position:
You deposit: 1 ETH + 2,000 USDC = $4,000
Your share: 0.01% of pool
You receive: LP tokens representing 0.01%
Fee Earnings:
Daily fees: $5,000,000 × 0.003 = $15,000
Your share: $15,000 × 0.0001 = $1.50/day
Annual: $1.50 × 365 = $547.50/year
APY: $547.50 ÷ $4,000 = 13.7%
But Wait: This doesn't account for:
Impermanent loss (could be -5% to -20%)
Gas costs for depositing/withdrawing
Price volatility reducing your ETH holdings
Net Result: Your actual return might be 5-8% APY, or even negative in volatile markets.
🔑 Key Takeaways
AMMs replace order books with mathematical formulas (x · y = k)
Liquidity pools hold reserves of two tokens
LPs earn fees from all trades, proportional to their share
Prices adjust automatically based on supply and demand
Capital efficiency is low in V2 - most liquidity sits idle
High APY numbers are misleading - they ignore impermanent loss
🚀 Next Steps
In the next lesson, we'll dive deeper into the mathematics, learning how to:
Calculate exact swap amounts
Understand price curves
Measure liquidity depth
Optimize your position size
But first, complete Exercise 1 to test your understanding of AMM fundamentals.
Remember: Understanding AMMs is the foundation. Master this before moving to advanced concepts like concentrated liquidity. The math gets more complex, but the fundamentals remain the same.
Last updated