Lesson 2: The Mathematics of Liquidity Provision

🎧 Lesson Podcast

https://storage.googleapis.com/liquidity-provision-media/lesson-02/audio/lesson2%20Automated_Market_Maker_Math_Constant_Product_Explained.m4astorage.googleapis.com

🎬 Video Overview

Lesson 2: The Mathematics of Liquidity Provision

🎯 Core Concept: Math is Your Protection

Understanding the mathematics behind AMMs isn't just academic—it's your primary defense against losses. The formulas determine:

• How much you'll receive when swapping

• What price impact your trade will have

• How fees are calculated and distributed

• Why impermanent loss occurs

Master these calculations, and you'll make better decisions, avoid costly mistakes, and optimize your returns.

📐 The Constant Product Formula: Deep Dive

The Fundamental Equation

$x \cdot y = k$

This simple equation governs every trade in a constant product AMM. Let's break it down:

Variables:

• x: Reserve of token X (e.g., ETH)

• y: Reserve of token Y (e.g., USDC)

• k: Constant product (must remain unchanged after fees)

Rule: After any trade (excluding fees), x × y must equal k.

Calculating Swap Amounts

When you want to swap Δx tokens of X for tokens of Y:

Without fees: $(x + \Delta x) \cdot (y - \Delta y) = k$

With fees (fee rate φ, e.g., 0.003 for 0.3%): $(x + \Delta x \cdot (1 - \phi)) \cdot (y - \Delta y) = k$

The fee is deducted from the input amount before the swap calculation.

Swap Calculation Step-by-Step

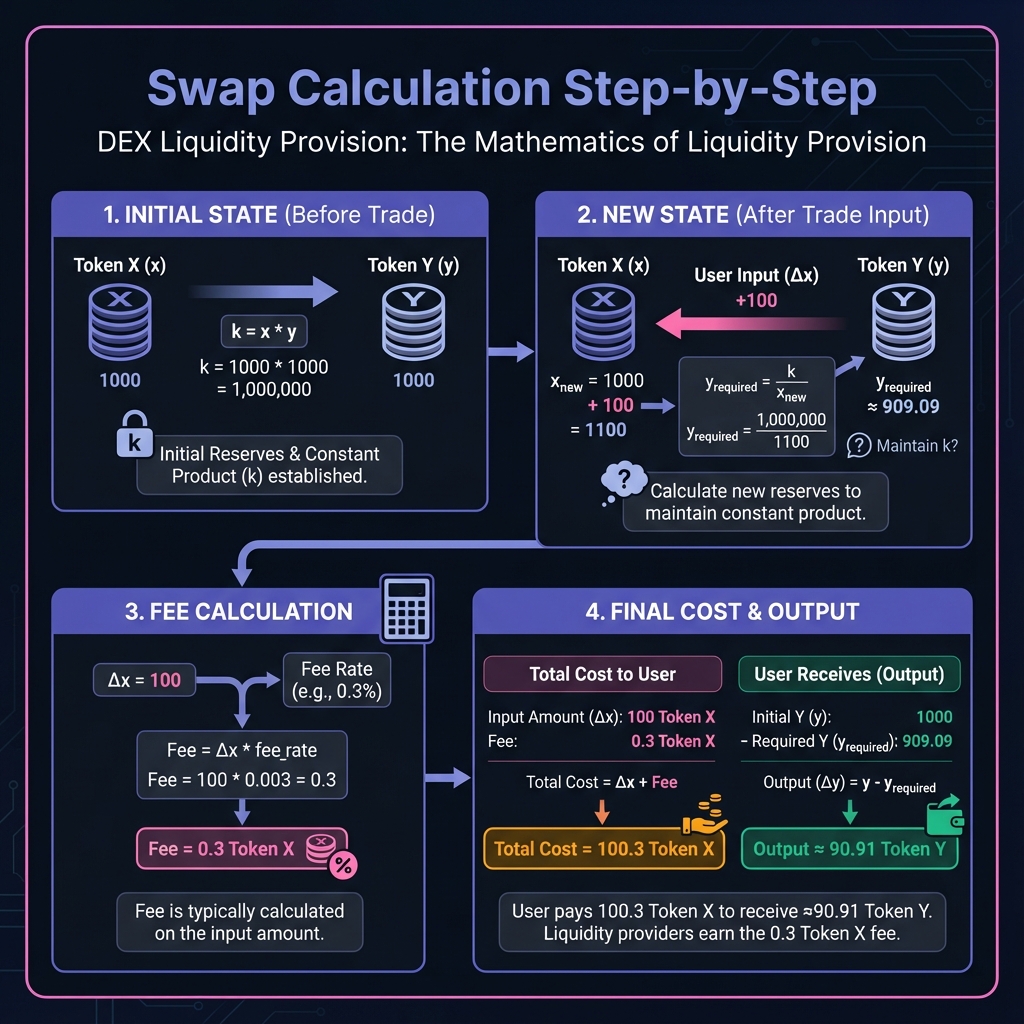
Step-by-Step Calculation

Example: Pool has 10 ETH (x) and 20,000 USDC (y)

• k = 10 × 20,000 = 200,000

• Fee rate: 0.3% (φ = 0.003)

• You want to buy 1 ETH with USDC

Step 1: Calculate new x after your trade

• x_new = 10 + 1 = 11 ETH

Step 2: Calculate required y to maintain k

• y_new = k ÷ x_new = 200,000 ÷ 11 = 18,181.82 USDC

Step 3: Calculate how much USDC you need to deposit

• Δy = 20,000 - 18,181.82 = 1,818.18 USDC

Step 4: Add fee (0.3% of input)

• Fee = 1,818.18 × 0.003 = 5.45 USDC

• Total you pay = 1,818.18 + 5.45 = 1,823.63 USDC

Result: You pay 1,823.63 USDC to receive 1 ETH

• Effective price: 1,823.63 USDC per ETH

• Original price: 2,000 USDC per ETH

• Price impact: (1,823.63 - 2,000) ÷ 2,000 = -8.8%

Price Impact Formula

The larger your trade relative to the pool, the more price impact:

$\text{Price Impact} = \frac{\Delta x}{x} \times 100\%$

For the example above:

• Δx = 1 ETH, x = 10 ETH

• Price impact ≈ 10% (simplified calculation)

Key Insight: Trade size matters. A $100,000 trade in a $1M pool will have significant impact. A $100 trade in the same pool will have minimal impact.

📊 Understanding Price Curves

The Hyperbolic Price Curve

The constant product formula creates a hyperbolic price curve:

Price Curve Visualization

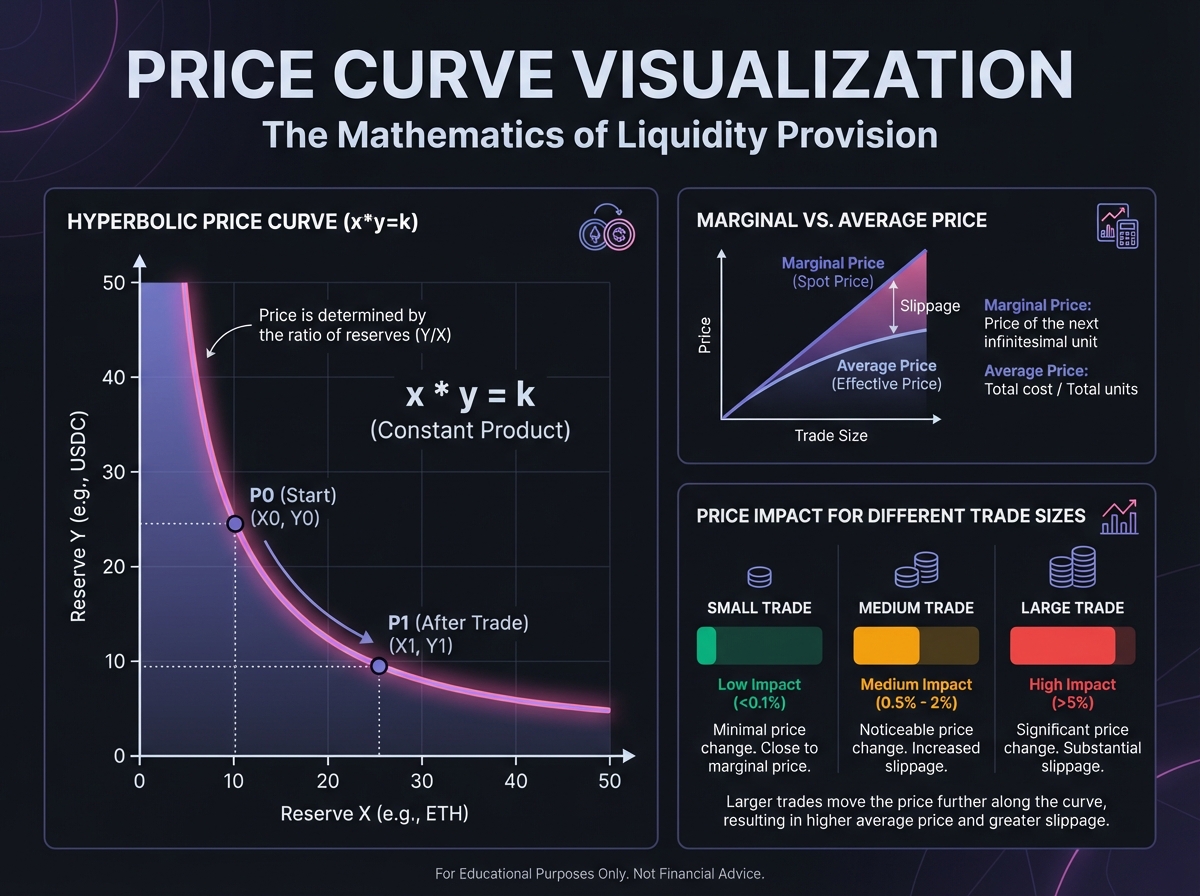
Characteristics:

• As x approaches 0, price approaches infinity

• As y approaches 0, price approaches 0

• The curve is always decreasing (more X = lower price of X)

• Price changes smoothly with each trade

Price Calculation

The current price of token X in terms of token Y:

$P = \frac{y}{x}$

Example:

• Pool: 10 ETH, 20,000 USDC

• Price: 20,000 ÷ 10 = 2,000 USDC per ETH

After buying 1 ETH:

• Pool: 11 ETH, 18,181.82 USDC

• New price: 18,181.82 ÷ 11 = 1,653 USDC per ETH

The price moved down because ETH supply increased (you added ETH to the pool by buying it).

Marginal Price vs. Average Price

Marginal Price: The price for the next infinitesimal trade

• Formula: P = y/x

• This is what you see on interfaces

Average Price: The price you actually pay for your trade

• Formula: (Total USDC paid) ÷ (ETH received)

• Always worse than marginal price due to slippage

Example:

• Marginal price: 2,000 USDC/ETH

• You buy 1 ETH for 1,823.63 USDC

• Average price: 1,823.63 USDC/ETH

• Difference: 176.37 USDC (8.8% worse)

💧 Liquidity Depth and Capital Efficiency

Measuring Pool Depth

Pool depth determines how much you can trade before significant price impact:

$D = \sqrt{x \cdot y} = \sqrt{k}$

Deeper pools (larger k):

• Can handle larger trades

• Less price impact per trade

• More stable prices

Shallow pools (smaller k):

• Large trades cause significant slippage

• Prices move dramatically

• Higher risk for LPs

Capital Efficiency Problem

In Uniswap V2, liquidity is distributed across the entire price curve (0 to ∞). For a stablecoin pair trading at $1.00:

• 99.9% of liquidity sits at prices like $0.01 or $100.00

• Only 0.1% is active near the current price

• This means 99.9% of capital earns no fees

Example:

• Pool: 1,000,000 USDC + 1,000,000 DAI (trading at 1:1)

• Active liquidity: ~$2,000 (0.1% of $2M)

• Idle liquidity: $1,998,000 (99.9%)

This inefficiency led to Uniswap V3's concentrated liquidity (Lesson 5).

Liquidity Depth Comparison Chart

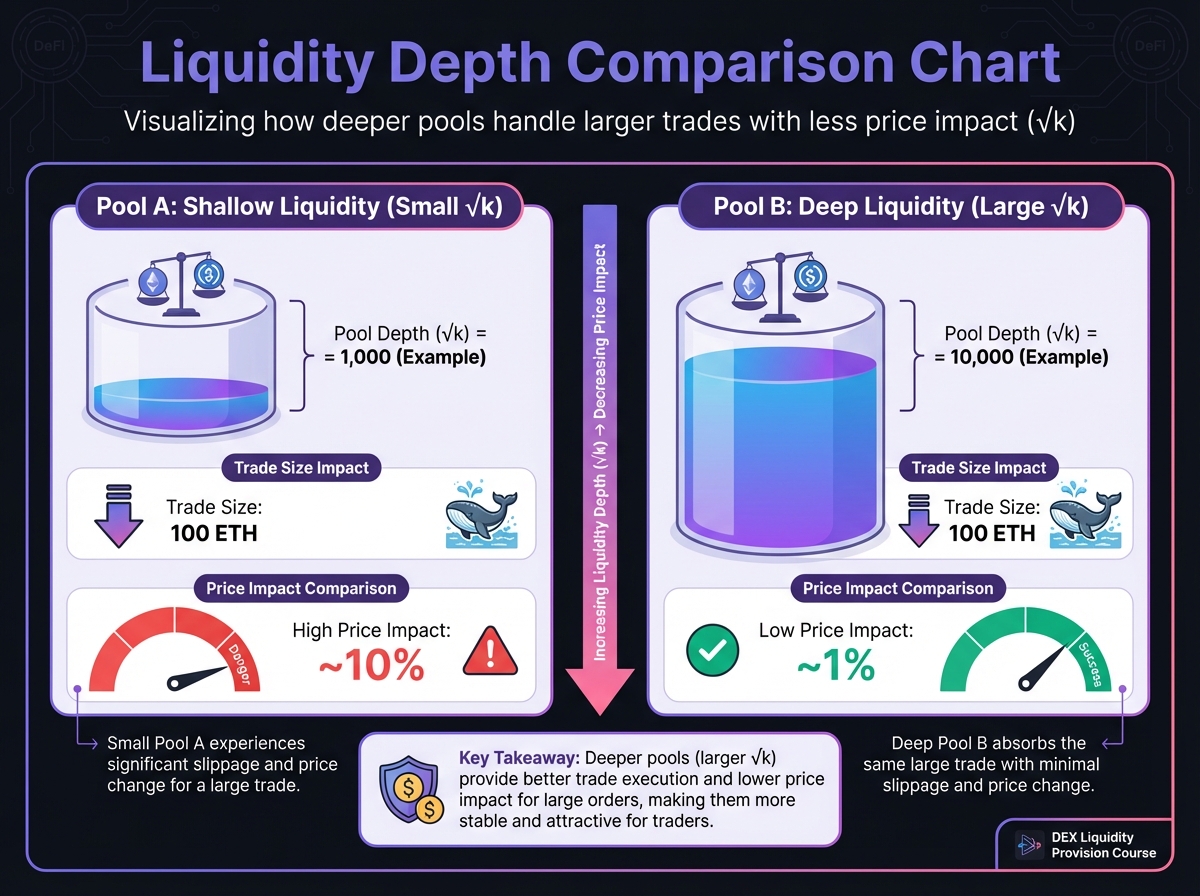
🧮 Fee Mathematics

How Fees Accumulate

Fees are added to the pool, increasing the value of LP tokens:

Before trade:

• Pool: 10 ETH, 20,000 USDC

• Your share: 10% (1 ETH, 2,000 USDC)

Trade occurs: Someone swaps 1 ETH for 1,823.63 USDC

• Fee: 5.45 USDC added to pool

• New pool: 11 ETH, 18,181.82 + 5.45 = 18,187.27 USDC

• Pool value increased by 5.45 USDC

Your new position:

• Still 10% of pool

• Value: 1.1 ETH + 1,818.73 USDC

• Gained: 0.1 ETH worth of fees (increased share)

Fee Distribution

Fees are distributed proportionally to LP token holders:

$\text{Your Fee Share} = \frac{\text{Your LP Tokens}}{\text{Total LP Tokens}} \times \text{Total Fees}$

Example:

• Total fees this week: 1,000 USDC

• Your LP tokens: 100

• Total LP tokens: 10,000

• Your share: (100 ÷ 10,000) × 1,000 = 10 USDC

APY Calculation (Simplified)

Daily Fee Calculation: $\text{Daily Fees} = \text{Daily Volume} \times \text{Fee Rate}$

Your Daily Earnings: $\text{Your Earnings} = \text{Daily Fees} \times \frac{\text{Your Capital}}{\text{Total TVL}}$

Annualized: $\text{APY} = \left(\frac{\text{Your Earnings}}{\text{Your Capital}} \times 365\right) \times 100\%$

Example:

• Daily volume: $1,000,000

• Fee rate: 0.3%

• Daily fees: $3,000

• Your capital: $10,000

• Total TVL: $1,000,000

• Your daily earnings: $3,000 × ($10,000 ÷ $1,000,000) = $30

• APY: ($30 ÷ $10,000) × 365 × 100% = 109.5%

⚠️ Critical Warning: This APY doesn't account for impermanent loss, which can easily exceed 100% in volatile markets!

Fee Accumulation Timeline

---

Interactive Fee Accumulation Calculator

Use this calculator to estimate your potential fee earnings and accumulation over time based on position size, pool TVL, volume, and fee tier:

Launch Fee Accumulation Calculator →

---

🔬 Advanced Deep-Dive: Mathematical Properties

Invariant Preservation

The constant product formula ensures the invariant k is preserved:

Proof: After a trade of Δx for Δy: $(x + \Delta x) \cdot (y - \Delta y) = x \cdot y + \Delta x \cdot y - \Delta y \cdot x - \Delta x \cdot \Delta y$

For small trades, Δx · Δy ≈ 0, so: $(x + \Delta x) \cdot (y - \Delta y) \approx x \cdot y = k$

Price Elasticity

The price elasticity of the pool determines how sensitive prices are to trades:

$\epsilon = \frac{\%\Delta P}{\%\Delta Q}$

Where:

• ε = elasticity

• %ΔP = percentage change in price

• %ΔQ = percentage change in quantity

For constant product AMMs, elasticity is always negative (price decreases as quantity increases).

Optimal Trade Size

To minimize price impact, traders should split large orders:

Single large trade: 10 ETH

• Price impact: ~50%

• Average price: 1,500 USDC/ETH

10 smaller trades: 1 ETH each

• Price impact per trade: ~5%

• Average price: ~1,900 USDC/ETH

• Better execution by ~27%

This is why aggregators like 1inch split orders across multiple pools.

📈 Real-World Calculation: Complete Example

Let's work through a complete example:

Pool State:

• ETH reserves: 100 ETH

• USDC reserves: 200,000 USDC

• k = 100 × 200,000 = 20,000,000

• Current price: 2,000 USDC/ETH

You want to: Buy 5 ETH

Step 1: Calculate new ETH reserves

• x_new = 100 + 5 = 105 ETH

Step 2: Calculate required USDC to maintain k

• y_new = 20,000,000 ÷ 105 = 190,476.19 USDC

Step 3: Calculate USDC needed

• Δy = 200,000 - 190,476.19 = 9,523.81 USDC

Step 4: Add 0.3% fee

• Fee = 9,523.81 × 0.003 = 28.57 USDC

• Total cost = 9,523.81 + 28.57 = 9,552.38 USDC

Results:

• You pay: 9,552.38 USDC

• You receive: 5 ETH

• Effective price: 1,910.48 USDC/ETH

• Price impact: (1,910.48 - 2,000) ÷ 2,000 = -4.5%

• New pool price: 190,476.19 ÷ 105 = 1,814.06 USDC/ETH

🎓 Beginner's Corner: Common Math Mistakes

Mistake 1: Assuming linear price relationships

• Wrong: "If 1 ETH = 2,000 USDC, then 10 ETH = 20,000 USDC"

• Right: Price changes with each ETH bought. 10 ETH might cost 25,000 USDC due to slippage.

Mistake 2: Ignoring fees in calculations

• Wrong: Calculating swap amount without fees

• Right: Always include fees (typically 0.3%) in your calculations

Mistake 3: Using average price as marginal price

• Wrong: "The price is 2,000, so I'll get 1 ETH for 2,000 USDC"

• Right: You'll pay more than 2,000 due to price impact and fees

Mistake 4: Not accounting for pool depth

• Wrong: "I'll trade $100k in this $10k pool"

• Right: Check pool depth first. Your trade might move price 50%+.

---

---

🔑 Key Takeaways

1. x · y = k governs all trades in constant product AMMs

2. Price = y/x determines the current exchange rate

3. Larger trades = more price impact due to the hyperbolic curve

4. Fees compound by increasing pool reserves

5. Pool depth (√k) determines how much you can trade

6. APY calculations are misleading without impermanent loss

🚀 Next Steps

Now that you understand the mathematics, Lesson 3 will show you the dark side: Impermanent Loss. This is where many LPs lose money despite earning fees.

Complete Exercise 2 to practice these calculations and build your mathematical intuition.

---

Remember: Math protects your capital. Master these formulas, and you'll make informed decisions. Ignore them, and you'll lose money to traders who understand them better.

← Back to Summary | Next: Exercise 2 → | Previous: Lesson 1 ←